Capturability Analysis for the Linear Inverted Pendulum Model via
Sum-of-Squares.
This was a project that was done for the EECS 598: Convex Optimization Methods in Control course taught by Professor Pete Seiler. It was done in collaboration with Grant Gibson and Jon Michaux.
Summary.
The objective of this project was to implement the outer approximation method from Posa et al [1]. We computed the 0-step and 1-step viable capture regions for a planar linear inverted pendulum model using Sums of Squares program and SDP. We were able to achieve similar results to the paper.
Introduction from the final report: “ Bipedal legged locomotion research has progressed greatly
over the past few decades. Many tasks such as walking,
running, and jumping have been successfully implemented
using legged robots. However, before any of these robots can
achieve complex motions, they must first learn to balance.
From the balance position, nearly all motions (including
shut down) are realized. For this reason, the design of safe,
balancing controllers is required in order to reduce failure
occurrence (which can also lead to hardware deterioration).
The crux of our research is the ability to design controllers
that guarantee safe dynamic bipedal locomotion.To prevent
failure modes (i.e. falling), controllers must be able to reject
unexpected external forces such as those which might arise
from navigating rough terrain. This process is known as
push recovery, and is essential for enabling bipedal robots
to exhibit multiple modes of locomotion in the real world
such as walking, running, and climbing stairs. In this report,
we reproduce the capturability approximation results for
the Linear Inverted Pendulum Model (LIPM) to achieve
push recovery. More explicitly, we implement the outer
approximation methods presented by Posa et al.[1] “
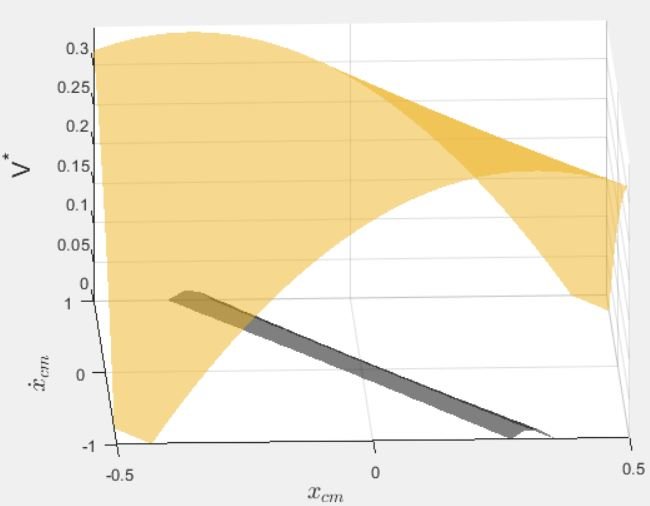
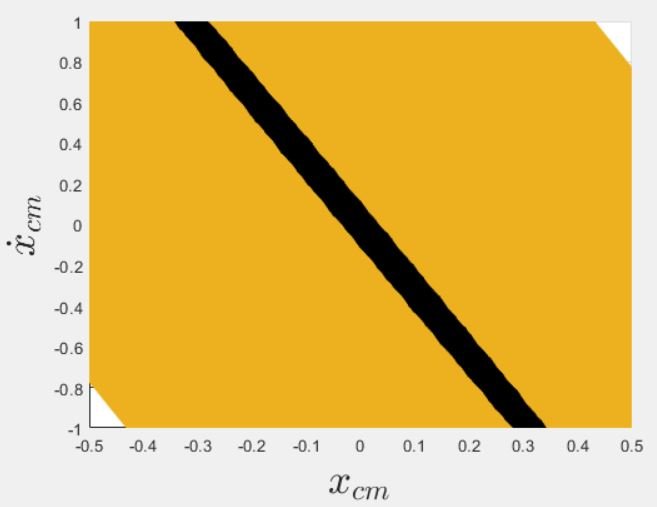
From the final report: “Outer Approximations for the LIPM. The top plot displays the three-dimensional
barrier function solution for the 0-step (black) and 1-step (orange) viable-capture
regions. The bottom plot is a top-down view of these functions.”
References
M. Posa, T. Koolen, and R. Tedrake, “Balancing and step recovery capturability via sums-of-squares optimization.” in Robotics: Science and Systems. Cambridge, MA, 2017, pp. 12–16